Fourier Transform Find inverse finite fourier sine transform of f(x) = (1cosnП)/n^2П^2 YouTube

Fourier Transform / Find the Fourier Transform of f(x) = e^(ax^2) YouTube

This function is called the box function, or gate function. It is shown in Figure 9.5.3. The Fourier transform of the box function is relatively easy to compute. It is given by ˆf(k) = ∫∞ − ∞f(x)eikxdx = ∫a − abeikxdx = b ikeikx|a − a = 2b k sinka. We can rewrite this as ˆf(k) = 2absinka ka ≡ 2absinc ka.

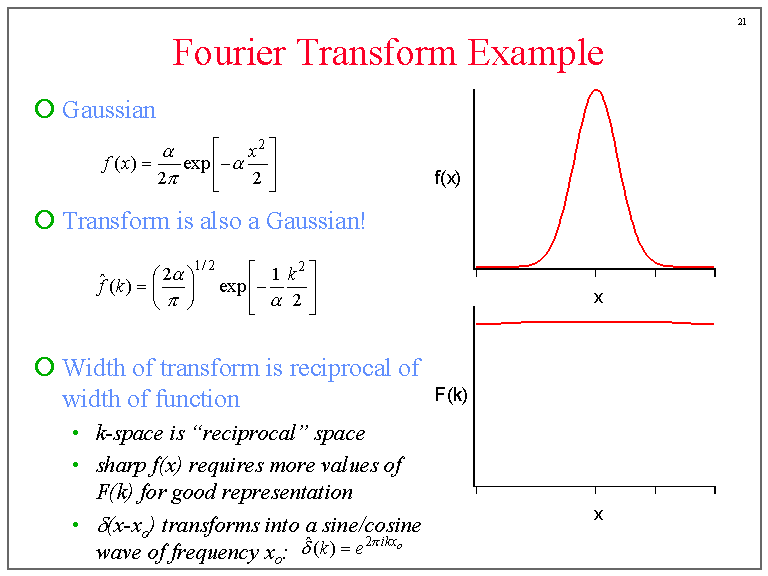
Fourier Transform Example

9 Fourier Transform Properties. The Fourier transform is a major cornerstone in the analysis and representa-tion of signals and linear, time-invariant systems, and its elegance and impor-tance cannot be overemphasized. Much of its usefulness stems directly from the properties of the Fourier transform, which we discuss for the continuous-time.

PPT The 2D Fourier Transform PowerPoint Presentation, free download ID3029981

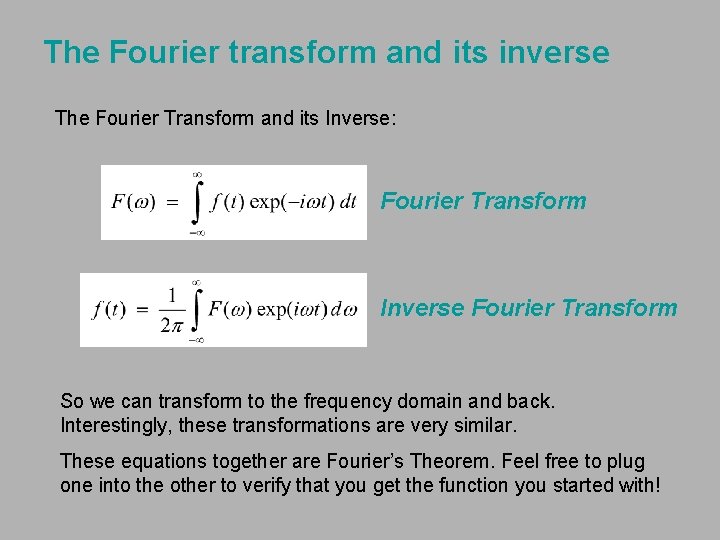
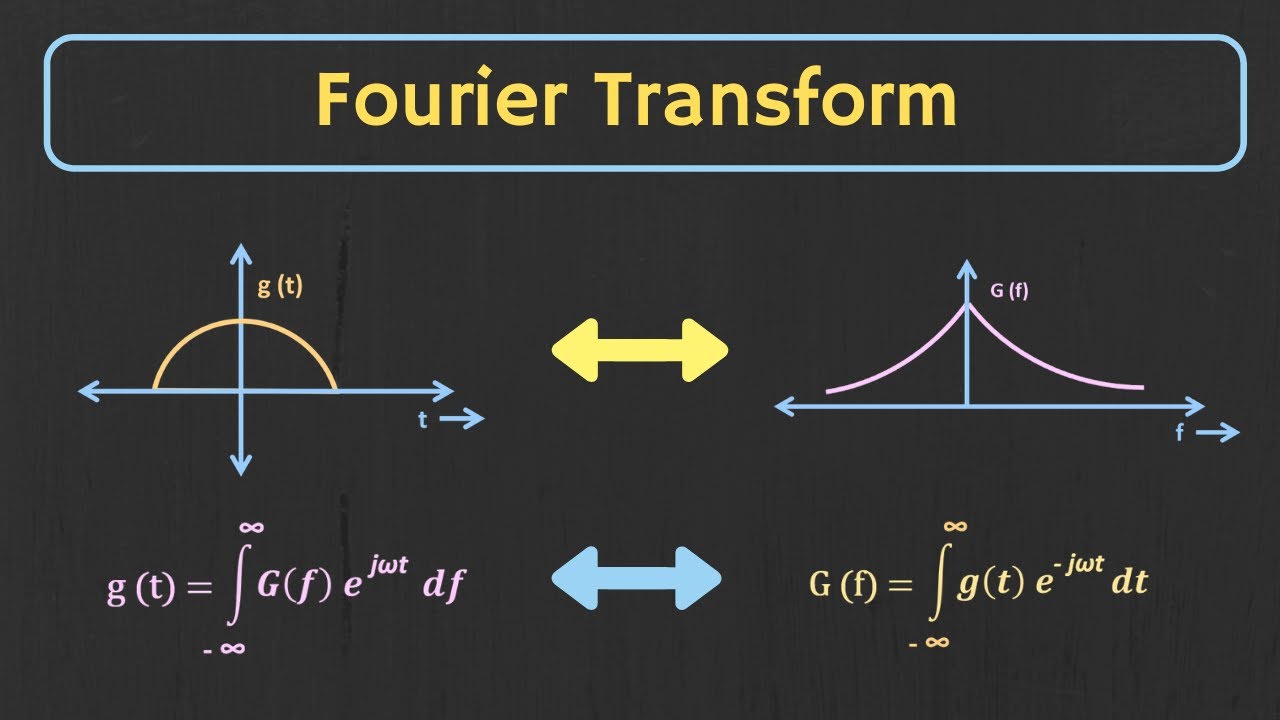
The Fourier transform is a generalization of the complex Fourier series in the limit as . Replace the discrete with the continuous while letting . Then change the sum to an integral , and the equations become. Here, is called the forward () Fourier transform, and. is called the inverse () Fourier transform. The notation is introduced in Trott.

PPT Chapter 3 DiscreteTime Fourier Transform PowerPoint Presentation ID6043318

Inverse Fourier Transform of the Fourier Transform. Ask Question Asked 5 years, 8 months ago. Modified 1 year, 2 months ago. Viewed 8k times. with absolutely integrable Fourier transforms. Share. Cite. Follow answered Aug 11, 2018 at 12:55. EditPiAf EditPiAf. 20.9k 3 3.

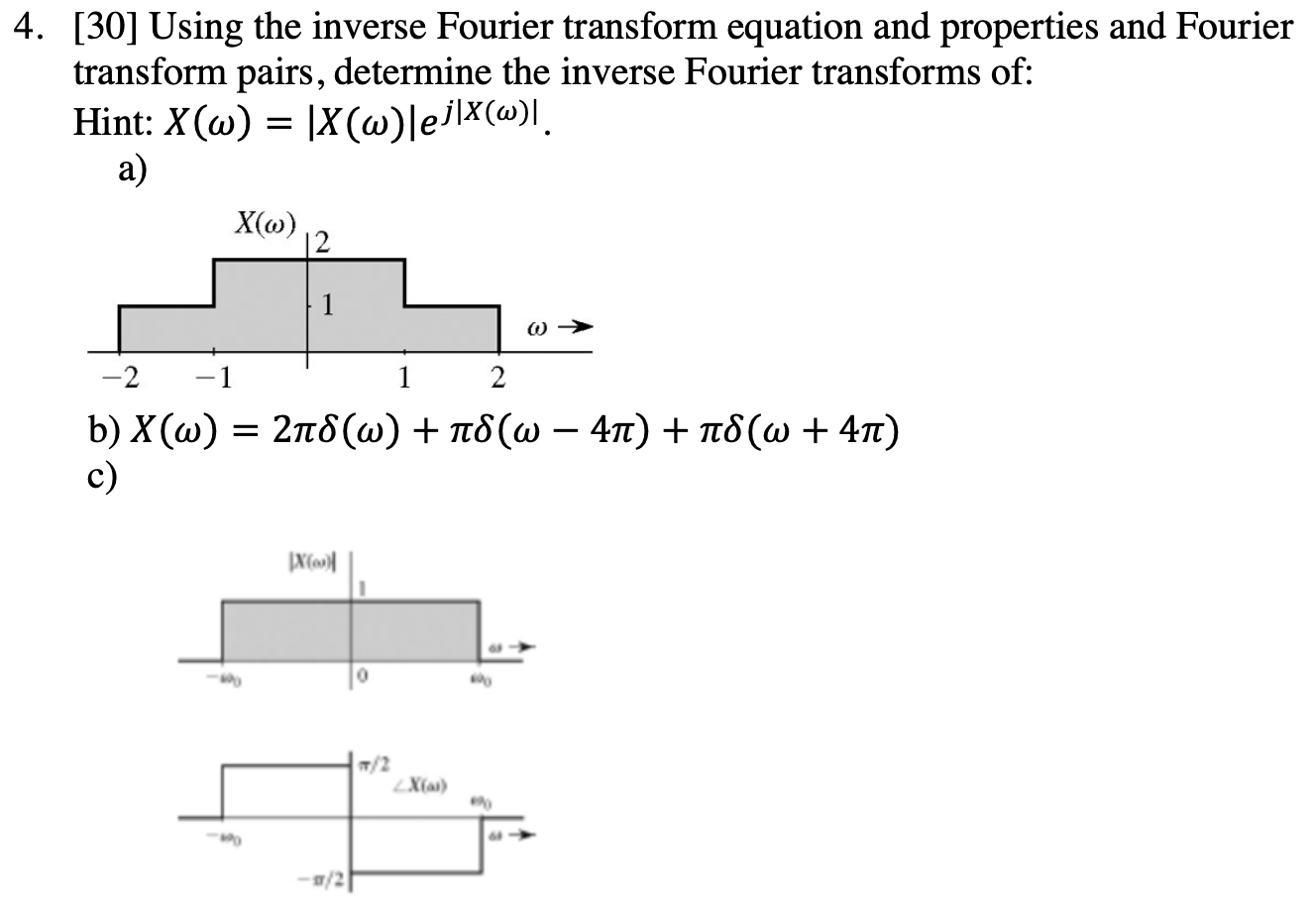
Solved 4. [30] Using the inverse Fourier transform equation

Fourier Transform" Our lack of freedom has more to do with our mind-set. Fourier Series representation is for periodic signals while Fourier Transform is for aperiodic (or non-periodic) signals. Consider an integrable signal which is non-zero and bounded in a known interval [− T 2; 2], and zero elsewhere. This signal will have a Fourier.

The Fourier Transform What is the Fourier transform

inverse Fourier transform. Have a question about using Wolfram|Alpha? Contact Pro Premium Expert Support ». Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music….

Fourier Transform Explained YouTube

Compute the inverse Fourier transform of exp(-w^2-a^2). By default, the independent and transformation variables are w and x , respectively. syms a w t. F = exp(-w^2-a^2); ifourier(F) ans =. exp(- a^2 - x^2/4)/(2*pi^(1/2)) Specify the transformation variable as t. If you specify only one variable, that variable is the transformation variable.

Solved 2. Determine the inverse Fourier transform of the

The calculation of the Fourier inverse transform is an integral calculation (see definitions above). On dCode, indicate the function, its transformed variable (often ω ω or w w or even ξ ξ) and it's initial variable (often x x or t t ). Example: ^f (ω)= 1 √2π f ^ ( ω) = 1 2 π and f(t)= δ(t) f ( t) = δ ( t) with the δ δ Dirac function.

PPT Lecture 11 PowerPoint Presentation, free download ID396272

The inverse Fourier transform is extremely similar to the original Fourier transform: as discussed above, it differs only in the application of a flip operator. For this reason the properties of the Fourier transform hold for the inverse Fourier transform, such as the Convolution theorem and the Riemann-Lebesgue lemma .

(a) Intensity and phase of the inverse Fourier transform of the... Download Scientific Diagram

Basic properties. In the previous Section 5.1 we introduced Fourier transform and Inverse Fourier transform ˆf(k) = κ 2π∫∞ − ∞f(x)e − ikxdx ˇF(x) = 1 κ∫∞ − ∞F(k)eikxdk with κ = 1 (but here we will be a bit more flexible): Theorem 1. F = ˆf f = ˇF . (Already "proved") . Theorem 2. Fourier transform.

Inverse shorttime Fourier transform MATLAB istft MathWorks 한국

Every function fis secretly a Fourier transform, namely the one of fq Note: This can also be written as f= F(fq ) fis the Fourier transform of fq In other words, the inverse Fourier transform undoes whatever the Fourier transform does, just like ex and ln(x) where eln(x) = x Note: The proof of this is quite hard, but follows by writing out F(fq )

PPT Fourier PowerPoint Presentation, free download ID496883

Definition The Fourier transform is an analysis process, decomposing a complex-valued function f (x) {\displaystyle \textstyle f(x)} into its constituent frequencies and their amplitudes. The inverse process is synthesis, which recreates f (x) {\displaystyle \textstyle f(x)} from its transform. We can start with an analogy, the Fourier series, which analyzes f (x) {\displaystyle \textstyle f(x.

The inverse Fourier transform YouTube

Fourier Transform (FT) and Inverse. The Fourier transform of a signal , , is defined as. (B.1) and its inverse is given by. (B.2) Subsections. Existence of the Fourier Transform. The Continuous-Time Impulse.

Inverse Fourier Transform of 1/(1+jw)^2 YouTube

The Fourier transform maps a function of time t to a complex-valued function of real-valued domain ω. Frequency plots provide intuition that is difficult to otherwise obtain. Find the Fourier transform of the following square pulse. X1(jω) = e ω 1 − e −ω 2. X1(jω) = sin ω ω ω. ω 2 X1(jω) = e − e −ω 4.

Solved 2. Determine the inverse Fourier transform of the

The Fourier transform of a function of x gives a function of k, where k is the wavenumber. The Fourier transform of a function of t gives a function of ω where ω is the angular frequency: f˜(ω)= 1 2π Z −∞ ∞ dtf(t)e−iωt (11) 3 Example As an example, let us compute the Fourier transform of the position of an underdamped oscil-lator:

What Is The Inverse Of A Fourier Transform Of A Sinc Function And The Images

the former, the formulae look as before except both the Fourier transform and the inverse Fourier transform have a (2ˇ) n=2 in front, in a symmetric manner. With the latter, one has ˚7! Z e 2ˇix˘˚(x)dx as the transform, and 7! Z e2ˇix˘ (x)dx as the inverse transform, which is also symmetric, though now at the cost of making the exponent.